
In this posting, David French makes excursion outside his field: patent law, to speculate on possible aspects relating to the physics and mechanism of the cold fusion phenomena.
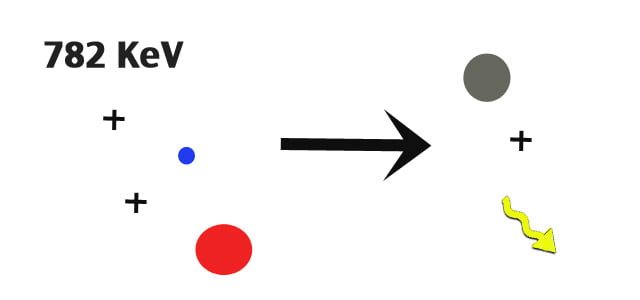
One of the theories to explain the ColdFusion excess energy effect is based on the premise that a proton can capture an electron, become a neutron, and then all sorts of magical things can happen. However, a neutron is heavier than the combined weight of a proton and an electron. The relative masses are:
Neutron = 1
Proton = 0.99862349
Electron = 0.00054386734
When you do the addition and subtraction it works out that a neutron is heavier than the proton-electron combination by a mass-energy equivalent of about 780 kilo electron volts ( keV). This amount of mass-energy must be found to make a neutron out of a proton and an electron. Here are some thoughts on that point.

When an electron falls from infinity towards a proton it acquires 13.6 electron Volts of energy to reach the ground state “orbital” around the proton. I have always wondered why it does not go all the way. Apparently, its Debroglie wavelength has to fit” around the “orbit radius” for it to occupy a stable state.
Perhaps another explanation is that an electron can only arrive in an atom and occupy an orbital by dissipating its arrival energy in the form of a photon. All the light we see originates from electrons settling into an empty slot in the shell of permitted orbitals around nuclei. If atomic dynamics do not permit the emission of such a photon, then an electron cannot settle into a stable orbital but must move on.
But what if an electron acquired enough energy to crash through the base orbital and proceed onward into a proton? How much more energy could the electron acquire hurtling towards the nucleus of a hydrogen atom? I have a suspicion that this might be a very large value if the radius of a proton is small enough.
Let us start by an analogy. Here is the formula for gravitational potential energy for a small mass “m” coming in from infinity to arrive at a radial distance “r” from a large mass M:
E = – GmM/r
This formula has an extraordinary consequence: if a mass were to fall to a point source where “r” drops to zero the energy would be infinite! This does not happen in the Sun, or even in the case of a penny being dropped down a very deep hole in the Earth. This is because as you go below the surface of the Sun or Earth the mass above you starts to cancel the gravitational force below you. Newton showed that there is no gravitational force at the center of the Sun or the Earth. The formula stops working when you reach a surface.
Let us turn to the potential energy associated with an electrical field. By integrating the energy acquired as an electron falls in from infinity, the amount of energy that it acquires as it approaches a proton is given by the following formula:
E = kQq/r
where Q and “q” are the sizes of the respective charges and “k” is a constant.
It will be seen directly that this formula parallels the one for energy acquired through gravitational attraction.
Again we are presented with the possibility that “r” might go to zero. Why is this important?
Well, Widom & Larsen postulate that an electron can be captured by a proton in order to become a neutron. But this requires approximately 780 keV, the mass difference between a neutron and the total mass of a proton and electron.
(I note that it has been said in Wikipedia about electron capture: “A free proton cannot normally be changed to a free neutron by this process; the proton and neutron must be part of a larger nucleus.” No reference is given for this statement.)
This large energy gap which is based on the mass difference between a neutron and a combined proton and electron has always seemed to me to be a barrier to electron capture by a proton. Since an electron only acquires 13.6 V falling from infinity to its ground state, it has got to acquire a lot more energy to get up to 780 keV. On the other hand, when “r” gets small, this kind of energy could be acquired quite quickly if the formula for potential electrostatic energy does not break down.
The gravity we experience from the Sun is the accumulation of force from the distributed mass contained in a body having substantial dimensions. It is not a point source. (Maybe a black hole is a point source!) But a proton is very nearly a point source. What does this size say about the potential energy that could be associated with the electrical attraction that extends between a proton and electron? Now let me take you on a little excursion concerning Blacklight Power and Randell Mills.
Randell Mills has his theory that electrons can occupy orbitals that are below the normal base orbital for a hydrogen atom. Randell calls such a special hydrogen atom a “hydrino”. Perhaps he has part of the explanation. I have met with Randell back in 1980’s and here is what he explained to me.
Electrons cannot fall below the base level in the normal hydrogen atom because they cannot emit a photon on their own. For his hydrinos to form there has to be a resonant absorption of energy from a nearby atom in order to permit an electron to drop below the normal base state. When falling through energy levels into an atom from infinity, an electron emits a photon to dissipate its acquired energy.
Apparently, once an electron reaches the base orbital, it is no longer capable of emitting photons as a way of losing energy. But according to Randell if a nearby atom is able to eject an electron, acting as a “catalyst”, it may serve to allow a proximate electron that is in the base orbital of a proton to fall to a lower energy level, closer to the proton. The energy that is associated with the electron falling through the electric field towards the proton is released through the resonant absorption of that energy by the nearby “catalyst” atom which disposes of the energy by ejecting one of its electrons. Here is a description of his theory from the web:
“According to Dr. Mills, when a hydrogen atom collides with certain other atoms or ions, it can sometimes transfer a quantity of energy to the other atom, and shrink at the same time, becoming a Hydrino in the process. The atom that it collided with is called the “catalyst”, because it helps the Hydrino shrink. Once a Hydrino has formed, it can shrink even further through collisions with other catalyst atoms. Each collision potentially resulting in another shrinkage.”
From the same source:
“For those of you with a mathematical bent, the formula is ((2 x n) -1) x 13.598 eV, where “n” is the level number. (BTW the maximum level number is certainly no larger than 137, and may well be less than that, not least because when a Hydrino gets very small, it may undergo fusion reactions with other atoms.) Of course, the numbers can be added up. IOW if you start with a Hydrogen atom, and end up with e.g. a level 5 Hydrino, then you get a total of 41 + 68 + 95 + 122 = 326 eV. The total for any level can be calculated with the formula (n^2 -1) x 13.598 eV.”
[End of quotation]
Well, 137 x137 = 18769 electron Volts and (n^2 -1) x 13.598 eV gives 18769 – 1 × 13.598 = 255,207.264 eV.
This is a value which is well on its way to 780keV!! I do not know why the limit in the above formula is 137, but let us accept that for the moment. Using the formula for the potential energy that becomes available when two electrically charged bodies are brought into close proximity to each other, namely E = kQq/r , it may be that this requisite energy condition is within reach of some force or effect originating from within the proton. At that moment, the magical conversion into a neutron may occur.
Maybe having fallen to level 1/137 an electron is able to fall further into a proton, eventually contributing the additional energy that it acquires into a quark conversion that changes the proton into a neutron of higher mass, and then the electron simply disappears!
On the other hand, there may be some other principle or limitation that would forbid such an event. Still, it is interesting to muse on the consequences an energy formula that includes the remarkable factor: 1/r.
Persons wishing to make comments on this posting are invited to visit the Cold Fusion Now website where this article is posted.

Attorneys should not make excursions into nuclear physics. This entire idea suffers from a basic misconception, even if hydrinos exist, which they almost certainly don’t.
If you consider a *system* of an electron and proton infinitely separated and both at rest, that system has a mass of 0.511 + 938.272 = 938.783 MeV/c^2.
It doesn’t matter what happens between them, that is the total mass (or energy) available to that system. It cannot increase its mass or energy (divided by c^2) or any combination of the two above 938.783 MeV/c^2 unless it exchanges energy with something outside the system. No matter what. At least to the extent that the conservation of energy is valid.
A neutron has a mass of 939.565 MeV/c^2. So, to make a neutron from an electron and a proton, the extra 782 keV has to come from outside the electron-proton system. It cannot come from the acceleration of the particles toward each other.
When two objects accelerate towards each other because of an attractive force (like gravity or the Coulomb force), the potential energy decreases (that’s why the potential energy formula has a negative sign), and the kinetic energy increases, but the energy of the system, and therefore its overall mass, does not change. When a photon is emitted corresponding to the 13.6 eV binding energy of the hydrogen atom, the mass decreases by that amount (divided by c^2), which is why a hydrogen atom has a mass 13.6 eV/c^2 less than the sum of an electron plus proton.
So the miraculous singularity of the 1/r dependence of the potential does not help you. If such an acceleration could happen, the potential energy would tend toward negative infinity while the kinetic energy tended toward positive infinity, but the system’s energy would stay the same. You can’t just make energy or mass outta nothing.
Electron capture by a proton requires an additional 782 keV. Pure and simple.
joshua cude, you said —–
“Attorneys should not make excursions into nuclear physics.”
I say, How pompous and arrogant can science get.
Rather than trying to make out one needs a degree in how to light a bunson burner to understand science you should celebrate that others are interested and with a little humility explain any errors that you think the person has made, in your opinion.
Scientists in many areas are incompetent and even corrupt, Cold Fusion is an example.
Science in all areas knows virtually nothing and yet tries to make out that they are experts.
Asking questions and looking for anomaly’s is sciences job and the answers must be based on Evidence and not “expert opinion” as they are in most of science.
On March 19, 2013 at 3:01 AM georgehants wrote:
“you said —–“Attorneys should not make excursions into nuclear physics.”
“I say, How pompous and arrogant can science get.”
But lawyers tell scientists not to practice law. In fact, they make it illegal for lay people to practice law.
I think it’s arrogant for someone with little or no training in physics to come along and tell physicists who spent a decade learning their stuff that they’re wrong about the amount of energy needed to produce a neutron from an electron and a proton. Especially when it’s clear they don’t understand the basic kinematics of such reactions.
It’s like a plumber presuming to diagnose your chest pain and offering to perform heart surgery using his pipe wrench and a blow torch.
Some things require training, and it’s simply arrogant to think that you can make a significant contribution in nuclear physics without first understanding what’s already been learned.
“Rather than trying to make out one needs a degree in how to light a bunson burner to understand science…”
You don’t need a degree, and bunsen burners have nothing to do with it, but nuclear physics is an experimental science. Without knowing the results of the experiments, and how they ft together, it’s hard to build on the knowledge. No one could come up with the idea that nuclear reactions exist out of thin air. People who promote cold fusion only know such a thing is even conceivable because all those corrupt conventional physicists discovered fusion for them. They discovered how it works in the sun, showed how it works in accelerators, made commercial neutron sources using fusion, and predicted and then showed muon catalyzed fusion, and predicted and demonstrated plasma fusion, calculated branching ratios and measured reaction products, and on and on.
And then the slow students of these experts come along and, failing to understand anything beyond that nuclear fusion releases energy with very little fuel, propose that it should work any damn place, because they want it to, and it would be so cool, and they call the experts idiots when the experts try to explain that they’ve misunderstood their lessons, and then try in vain for 24 years to achieve vindication. And never in all that time can anyone find a single experiment that a qualified scientist can perform with expected results (other than null results), even on a statistical basis. There is not a single nuclear reaction that people in the field can agree is occurring. There is not a single example of unequivocal energy density that exceeds chemical. There is not a single credible example where the energy from cold fusion can power the experiment itself, let alone the world.
”Scientists in many areas are incompetent and even corrupt, Cold Fusion is an example.”
People in many areas are incompetent and corrupt. And yes, cold fusion is an excellent example. Rossi, Dardik, Godes, and Mills are almost certainly corrupt. Celani, McKubre, Storms, and Piantelli, more likely fall into that other category.
”Science in all areas knows virtually nothing and yet tries to make out that they are experts.”
I don’t know what that means. An expert is just someone who knows more about something than most other people. And whatever you mean by “virtually
nothing”, scientists do know enough about solid state transistors and such to build iPhones. And they know enough about medicine to do heart transplants, and enough about gravity and space to land on the moon. And so on. And the people who do these things *are* experts. It’s how we define the word. You, on the other hand, are not an expert in writing, e.g., because your writing almost never makes sense. And this post is a good example.
“People in many areas are incompetent and corrupt. And yes, cold fusion is an excellent example. Rossi, Dardik, Godes, and Mills are almost certainly corrupt. Celani, McKubre, Storms, and Piantelli, more likely fall into that other category.”
Your statements are unsupported by evidence.
You are a known anti-cold fusion activist, who has no firsthand knowledge in any of these labs, ironic, given the content of your comment.
I require you to refrain from these types of accusations. There is no libeling scientists on Cold Fusion Now.
Any further personal attacks that go beyond the scientific issues presented here will be deleted.
“Any further personal attacks that go beyond the scientific issues presented here will be deleted.”
So, it’s ok to imply as George did that all scientists who are (or have been) actively skeptical of cold fusion are incompetent or corrupt, which would include scientists like Koonin, Lewis, Huizenga, Morrison, Seaborg, and others, as long as no names are mentioned?
Ruby has commented on the tone of permitted comments. I regret the excursions into unacceptable allegations that have been made. Fair warning has been given. But “Joshua Cude” does have a lot of information to impart. For that we can thank him. However, he is in error on one critical point.
He says: “There is not a single example of unequivocal energy density that exceeds chemical. There is not a single credible example where the energy from cold fusion can power the experiment itself,….” This is simply not true. It is fair to say that a process of “cold fusion” in terms of a fusion mechanism has not been conclusively demonstrated. The mechanisms are still unknown. But there are numerous conclusive demonstrations of “unexplained excess heat” that could not have originated from a chemical origin. And I believe there are numerous cases of self-sustained events, albeit for transient periods, that qualify as self-powered reactions.
Mr Cude is so assertive that others are wrong. Yet he is blind to evidence that he insists does not exist. Perhaps if he were to say: “I haven’t examined the relevant reports and therefore I can say that I see no evidence of a single example of unequivocal energy density that exceeds chemical. I know of no single credible example where the energy from cold fusion can power the experiment itself,….”, then we could respect his scientific integrity.
Self-sustained “Heat-after-death” occurred early on with Fleischmann and Pons and Tadahiko Mizuno and have continued since.
On March 19, 2013 at 5:26 PMDavid French wtoe:
“But there are numerous conclusive demonstrations of “unexplained excess heat” that could not have originated from a chemical origin. ”
No. There aren’t. There are numerous claims of such demonstrations, and some people conclude that they could not have a chemical origin. That’s not the same as “conclusive demonstrations” as I understand the words. A conclusive demonstration is one in which all or nearly all qualified observers agree on the conclusion.
But we saw in 1989 what happens when qualified scientists think there just *might* be evidence for anomalous heat from metal hydrides. It was front page news in all the papers, Nature and Science made time and room for the imminent tell-all publications, scientists stampeded to their labs to try to get a small slice of the glory for themselves, and Pons got a standing ovation from thousands of scientists. That’s not really happening now, because the vast majority of experts don’t believe there is conclusive evidence. And that includes expert panels enlisted to examine the best evidence, and reviewers and editors at prominent journals (like Science, Nature and PRL) that continue to reject papers, and reviewers for funding agencies that continue (for the most part) to reject funding requests.
If there were even one conclusive demonstration (which would be one that others could reproduce), it would be celebrated universally.
“And I believe there are numerous cases of self-sustained events, albeit for transient periods, that qualify as self-powered reactions.”
Nothing could be easier to demonstrate to a skeptical audience than a self-sustained event that exceeded chemical heat. Just isolate the core undergoing the phenomenon, and watch the temperature climb. What an easy way to convince the DOE panel that cold fusion or LENR is real. As cold fusion’s most loyal proponent (Rothwell) put it: “It is utterly impossible to fake palpable heat…. I do not think any scientist will dispute this. …An object that remains palpably warmer than the surroundings is as convincing as anything can be..” Since scientists still do dispute cold fusion, it would seem such a demo has not yet been realized. Anecdotal claims from people with a stake in it are not persuasive.
“Mr Cude is so assertive that others are wrong. ”
Yes, perhaps my language is a little over the top. Maybe it’s frustration. I’ve been watching the field a long time, and express this challenge frequently, and I used to do it more diplomatically, but no one ever actually gives an example that proves the claims wrong, so I have become bolder. I notice that you didn’t mention any specific examples. When pressed for a specific result, Rothwell usually falls back on McKubre’s 1994 electrolysis paper that claims 10.5 watts out with 10 watts in, not exactly earth shattering, especially when it was intended to validate P&F claim of 160 W out with 40 W in, but with better calorimetry. Instead, it showed that what P&F observed was probably all artifact (within uncertainty), and it would be a remarkable coincidence (one of many in this field) if the dramatically smaller effect McKubre saw was not a real effect.
If there were a real effect, after 24 years, you would think that there would be one experiment that anyone could do and get a consistent result, even if it is only on a statistical basis, and even if it requires centralized preparation of the metal in question, but nothing like that exists, and the MFMP demonstrates just how far we still are from that.
Another LENR patent granted… the energy to overcome… comes from somewhere. Perhaps the energetics are focused by harmonics within the lattice creating ‘superwaves’ .
Patent EP1656678B1 “Pulsed Low Energy Nuclear Reaction Power Generators”
Inventors: Herman Branover, Irving Dardik, Arik El-Boher, Dan Gazit, Ehud Greenspan, A. Boris Hachaturov, Vitaly Krakov, Shaul Lesin, Gad Shani, Tatyana Zilov
Assignees: Energetics Technologies, Llc
Patent number: EP1656678B1 – Filing date: Aug 12, 2004 – Issue date: May 4, 2011
“[0021]
According to the invention, there is also provided a method for generating a low energy nuclear reaction involving a material and hydrogenous atoms, the method being implemented on a low energy nuclear reaction cell containing an electrically conductive electrolyte having enveloped therein an anode-cathode electrode pair, the cathode electrode being formed of the material, the method comprising: applying across the electrode pair a train of pulsed electrical packets, to cause a correspondingly pulsed current to flow between the electrode pair, causing the electrolyte to dissociate, whereby oxygen is released at the anode electrode while the hydrogenous atoms migrate toward the material cathode electrode, each packet of pulses producing a surge of the hydrogenous atoms which are forced into the material cathode electrode, successive surges producing a dense packing of the hydrogenous atoms in the material cathode electrode; characterized in that: a cluster of pulses is superimposed on each packet; and each pulse in the cluster of pulses has a maximum amplitude that is proportional to an instantaneous amplitude of a major wave associated with the train of pulsed electrical packets, and wherein each pulse in the cluster of pulses has a maximum frequency that is proportional to an instantaneous frequency of the major wave associated with the train of pulsed electrical packets.
[0022]
Preferable features are set out in the dependent claims.
[0023]
A significant feature of the present invention which distinguishes it from prior cells in which the current through the electrolyte is pulsed, is that in a cell in accordance with the invention, pulsing takes place in a pulse pattern that increases the probability of LENR to occur and, hence, the level of reproducibility.”
[0078]
“In a generator in accordance with the invention, a resistance meter (LCR) 21, which may include a second modulator 20 and a voltmeter 22, may be implemented in order to measure the resistance of cathode 12. This measurement may then be used to indicate the level of deuterium atom-packing of the cathode.
[0079]
Highly effective computer pulse pattern programs afford optimum results, resulting in the greatest amount of nuclear reaction heat at the palladium electrode. These can be determined empirically by modifying the program of computer 16 to find the most effective pattern and by modifying the program to be responsive to the resistance of the cathode measured by LCR 21. In one example of a method according to the present invention, the change in resistance may be used to modify the modulating in order to maximize the atom-packing. A feedback signal representing the slope of the resistance, for example, may be used to optimize the relationship between any of the waves with respect to any of the other waves, the respective frequencies of the individual waves, the respective amplitudes of the individual waves, or any other suitable parameter.
[0080]
One example of the most effective pulse pattern is to incorporate a relaxation period corresponding to the downward phases of the major wave W1. Pulse packets in the pulse train may be completely turned off during the relaxation periods corresponding to the downward phases. FIG. 4 illustrates a pulse pattern with pulses (e.g., pulses of packet II, FIG. 3) completely switched off during the relaxation period.
[0081]
The program is developed from a formation of superwaving waves which are digitized so as to derive a pulse at the peak of each wave cycle. The aforementioned Dardik article illustrates various forms of superwaving waves.”
joshua, you have put up a very long reply to confuse the issue.
I will ask you a question so that all may judge your general scientific competence.
Would you please put a up a short concise reply explaining what science can say about the possibility of the World being intelligently designed.
Thank you
Thankyou for your response and for your clarity. I did not post as an attorney but as a student of the Cold Fusion mystery, albeit a naive one.
Your matching an emitted photon (with an energy corresponding to the binding energy of 13.6 eV) to the mass difference of 13.6 eV/c^2 between a hydrogen atom and the sum of an electron plus proton is interesting. Releasing a photon decreases the mass of the remaining components of the system.
It would appear that Widom & Larsen really do have to scrape-up 780keV for their heavy electron to form a neutron.
I appreciate your contribution.
Suggest reading all of WL papers, including;
“ULM neutron production can begin in a given many-body ‘patch’ after local E-field strengths exceed 2 x 10^11 V/m (i.e., e* mass renormalization ratio β is now greater than the minimum threshold ratio β0) and an adequate number of mass-renormalized e* electrons have been created (enabled by local breakdown of the Born-Oppenheimer approximation in ~temporal conjunction with nonequilibrium energy inputs).”
Ref: http://www.newenergytimes.com/v2/sr/WL/slides/20120229LatticeEnergyDoc.pdf
This field strength is 2.7 x 10^5 times the 780KeV you’ve pretended was unavailable.
W&L give no evidence for any of their conjectures, and the theory has got very little support among other theorists *within* the cold fusion community, and none at all outside it. The theory replaces a Coulomb barrier less than 100 keV with a hard energy barrier of 780 keV, which is why it is like jumping from the frying pan into the fire as explained by a working nuclear physicist (Thieberger) in this document: http://www.scribd.com/doc/83026935/Cold-Fusion-and-LENR. As he says, the theory is totally beyond any reasonable credibility. Which is presumably why after 6 years or so, no one of any distinction has even noticed it. If it had merit, WL would be given Nobel prizes.
Your last statement compares two different physical quantities (field strength and energy) that have different dimensions, and is therefore nonsense.
In any case, I entered the discussion because the title argument claimed that the 780 keV (external) may not be needed, and that is also what you tried to argue. I argued that it *was* needed, not that it was unavailable, although there is certainly no evidence that it is.
LENR is an observational science not requiring proof of fundamentals. Like gravity, no fundamentals exist since the Newton created the gravity equation. Newton’s 1713 General Scholium in the second edition of Principia: “I have not yet been able to discover the cause of these properties of gravity from phenomena and I feign no hypotheses… It is enough that gravity does really exist and acts according to the laws I have explained, and that it abundantly serves to account for all the motions of celestial bodies.”[34]
1.No fundamental proof is required to do observational science. Even the best physicists have not a valid gravity cause after 300 years.
2.You fell into my trap of you pretending field strength does’t matter. High potential over a short distance can deliver high energy. No fundamental mechanism or proof required.
3.Hot fusion has not reached break even in 50 years, why your short fuse standard against LENR?
4.Jet NANOR demonstrates up to 16 to 1 heat yields. Excellent observational science, closed cell simple devices for 6 months+.
So, joshua crude why push FUD here trying to prevent observational science progress? Are you funded by fossil fuels, military, or competing research? Is your job insecure or are you looking for work in these fields? Are you under the illusion that equations explain it all and there is nothing left to learn? What motivates you to promote FUD rather than science?
On March 20, 2013 at 2:23 AMJob001 wrote:
“1.No fundamental proof is required to do observational science. Even the best physicists have not a valid gravity cause after 300 years.”
The answer to life the universe and everything may elude us always, but a great deal *has* been learned about gravity since Newton. GR explains many things Newton’s theory can’t, including detailed motion of planets such as the perihelion precession of mercury.
“2.You fell into my trap of you pretending field strength does’t matter. High potential over a short distance can deliver high energy.”
Not the 5 orders of magnitude above 780 keV that you claimed though. (but nice try covering your ass)
“3.Hot fusion has not reached break even in 50 years, why your short fuse standard against LENR?”
Cold fusion is not supposed to be like hot fusion. If it were, what’s the excitement about?
Many skeptics of hot fusion, who oppose its support, are also skeptical of cold fusion and oppose its support as well.
But the fact remains that hot fusion *has* demonstrated fusion unequivocally, and can describe the reaction in detail. That puts it miles ahead of cold fusion and if you measure time in experimental iterations, cold fusion is already hundreds of times older.
“4.Jet NANOR demonstrates up to 16 to 1 heat yields. Excellent observational science, closed cell simple devices for 6 months+.”
Right. Milliwatts. And where is this brilliant work published? Not in any peer-reviewed journal I’m aware of.
And to whom is it demonstrated? To classrooms of newbies. Why don’t they take their 6-month demo and show it to the DOE?
“Are you funded by fossil fuels, military, or competing research?”
All of the above. Because all it takes to suppress scientific revolutions is a good argument on an internet forum. Everyone knows that.
“Are you under the illusion that equations explain it all and there is nothing left to learn?”
If that were true, then there would be no motivation for competing research, and therefore no reason to pay me the big bucks. So, no.
“What motivates you to promote FUD rather than science?”
I don’t. I promote science rather than evidence-free pseudoscience.
Joshua, You seemed to have failed to answer my above question so that I can judge your general scientific abilities.
Please answer.
Thank you.
Ideas about the Randell Mills “hydrino’s” have been given on e-Cat Site in the article “Cold fusion Catalyst”. Hydrino’s have never been detected by mass spectrography. As far as I know neutrons are split off in particular fission and fusion reactions but not formed by reacting a proton with an electron.
A proton has a non-zero radius (see equation on pages 3-4 of Belgian Patent 1002781, translated into English on e-Cat Site in the article “LANR by Coulomb explosion” to which patent exists a sequel text describing the use of positively charged liquid lithium (at kev voltage) into which deuterons (D-) are projected . An aneutronic reaction can take place with (H-) adsorbed on lithium particles . Have a look at the Swedish Defence article on LENR News or Cold Fusion Times.
Thanks David for pointing out that an incredible 780 KeV of energy would be needed to create a neutron. This is why I like F&P’s original idea that a heavy electron could be BORROWED from and then returned to the conduction band (I presume) to behave like a muon in muon catalyzed fusion (not consumed to form a neutron). This is how Richard K. Lyon explained it in his May 15, 1989 letter to C&E News (a few weeks after F&P’s March 23, 1989 press conference):
“….From the media accounts, the Pons and Fleischmann experiment appeared to have been motivated by the speculation that since electrons in a conduction band move collectively, it is possible for a conduction-band electron to act as if it were much more massive than a free electron. Thus, if there is a dislocation in the matrix of palladium ions, a site at which occupancy by two deuterium ions is marginally possible, an electron between these two deuterium ions might, by virtue of is effectively greater mass, bring them close enough for fusion to occur.The contradiction between the observed large heat release and the very small neutron yield may be explained by making the further assumption that catalyzed cold fusion is a different process from thermal fusion. In thermal deuterium-deuterium fusion the 4He nuclei is an extremely short-lived intermediate; the two deuterons come together with both the energy of the reaction and the thermal energy needed to overcome the coulombic barrier. This thermal energy brings with it considerable angular momentum. Since the 4He nuclei is isolated, the only ways in which it can dispose of the excess energy and angular momentum are by decomposition to 3He + n and to T + H. In catalyzed cold fusion, however, the situation is quite different. The 4He nucleus is formed without significant angular momentum or thermal energy and is not isolated in that the electron which catalyzed the fusion event is available to remove excess energy.
Thus one possible explanation for the production of heat without corresponding neutron production is that when fusion is catalyzed by conduction-band electrons in palladium the dominant reaction is to 4He, with 3He + n and T + H only minor side reactions….”
Richard K. Lyon May 15, 1989 letter to C&E News
Firstly, higher effective mass of electrons in solid state materials refers to their reduced mobility as they move in the conduction band, not an actual increase in inertial mass. In order to screen the proton charge, as in muon-catalyzed fusion, its wave function has to become localized near the proton, as in an s-orbital. In this case, the collective conditions that give it a higher effective mass disappear.
Secondly, branching ratios in muon-catalyzed fusion are exactly the same as in ordinary thermal fusion, so the arguments that they should be different if catalyzed by a “heavy” electron fail, quite apart from solid kinematic energy and momentum conservation arguments that make the absence of neutrons and protons a vanishingly remote possibility.
Good points Joshua. What do you think is happening? Do you think some sort of nuclear reaction is taking place?
Yes, it may be more difficult for heavy electrons to form at room temperature but they do aggregate readily at low temperatures. http://www.princeton.edu/main/news/archive/S33/94/41S36/
P.S.
Also, neutron emission has been seen when a titanium-deuterium system is cooled in liquid nitrogen. http://link.springer.com/article/10.1007%2FBF02844876?LI=true#
“No Core Shell Model for Nuclear Structure and Reactions”
B.R. Barrett, S. Quaglioni, I. Stetcu (UA) P. Navratil, W.E. Ormand (LLNL), J.P. Vary (ISU), A. Nogga (FJ)
http://www.phy.anl.gov/theory/ria06_pdf/barrett.pdf
This sounds a lot like the Hydrino discribed by Randal Mills.
There we go again pretending with bad assumptions. The assumptions regarding a lattice are not the unshielded assumption for electrons and protons isolated in a vacuum!
Were it so, transistors would not exist since “tunneling” could not happen. “Tunneling” happens because the “coulomb” barrier energy(all or in part) isn’t required due to forms of ” lattice shielding”, perhaps you describe it differently, and i couldn’t care less.
Likewise, shielding due to multi body mobile electron and proton fields happen and overcomes the coulomb barrier nonsense. Likewise also, whether a true neutron forms may be in question. It may be that these reactions happen due to quasi neutrons formed by virtual electrons mirror imaged in the free electron lattice clouds.
What we surly know is that the tough spectroscopic science needs to be done to clarify what is real data rather than going back and doing another pretend coulomb magic barrier seance (782 keV pure and simple crap assumption) against this excellent new science.
It’s all about the right assumptions and explaining the experimental data.
It’s NOT about ignoring the data and insisting on the WRONG assumptions!
“The assumptions regarding a lattice are not the unshielded assumption for electrons and protons isolated in a vacuum!”
Nuclear reactions have been studied in every phase from vacuum to gas to liquid to solid to plasma. In particular, fusion reactions in palladium hydride have been extensively studied, and are used in commercial neutron sources. Nuclear reactions were first discovered in the solid phase, and fission reactors generate energy by nuclear reactions in solid uranium dioxide. Radioisotope thermoelectric generators are all about nuclear reactions in the solid phase. Physicists are familiar with solids, and make no assumptions about the vacuum when they consider cold fusion.
“Were it so, transistors would not exist since “tunneling” could not happen.”
Wow. You’re wrong coming and going. Most transistors do not depend on tunneling, and tunneling does not need a lattice.
“Tunneling” happens because the “coulomb” barrier energy(all or in part) isn’t required due to forms of ” lattice shielding”, ”
No. That’s wrong. Tunneling does not require shielding. Electrons in a lattice can provide shielding, which reduces the Coulomb barrier, but it is not needed for tunneling. Essentially all fusion in the sun occurs because of tunneling, since surmounting the classical barrier requires energy vastly higher than the nuclei possess in the sun. Look up quantum tunneling in Wikipedia.
“Likewise, shielding due to multi body mobile electron and proton fields happen and overcomes the coulomb barrier nonsense.”
The Coulomb barrier is not nonsense, and according to calculations that *assume* a lattice and take account of multi-body fields, the barrier still limits fusion rate to about 30 orders of magnitude too low to produce measurable heat. And so far, no evidence for fusion in non-radioactive metal hydrides has been generally accepted.
“Likewise also, whether a true neutron forms may be in question. It may be that these reactions happen due to quasi neutrons formed by virtual electrons mirror imaged in the free electron lattice clouds.”
Sure. Whatever. You can use those terms like abracadabra, but it doesn’t make any sense. Magic may happen, but unless you can find evidence to support your quasi neutrons and mirror images of virtual electrons, it’s just gibberish and fuzzy thinking.
“What we surly know is that the tough spectroscopic science needs to be done to clarify what is real data”
What have the researchers been doing for the past 24 years?
“rather than going back and doing another pretend coulomb magic barrier seance (782 keV pure and simple crap assumption) against this excellent new science.”
Most serious cold fusion researchers are not claiming a violation of the conservation of energy, and in that case the 782 keV required to make a neutron from a proton and an electron is not a crap assumption. The total energy content of a neutron is 782 keV higher than that of an electron plus a proton. There is no tunneling effect, or screening effect or any other solid state effect that can make that need for energy go away. If you don’t understand that, you need to study a little.
By the way, D-D or D-T fusion only takes about 50 keV energy because of tunneling, because that’s an exothermic reaction, and that barrier *can* be reduced by screening (witness muon-catalyzed fusion), again because it’s exothermic.
“It’s all about the right assumptions and explaining the experimental data.”
Skeptics are capable of taking lattice effects into account, and do, and with those considerations, there is no compelling experimental data that suggests nuclear reactions in metal hydrides.
You illustrate well the issue of making poor assumptions and ignoring current research.
1.Extremely little relevant spectroscopic work has been done before 2005 due to lack of suitable modern instruments and poor assumptions that calorimetry was sufficient and suitable.
2.Ignoring current and quoting obsolete research to support your crap bias assumptions is not science.
3.Presuming i’m wrong about anything flies in the face of reality, i didn’t propose anything other than your extreme old school bias while pointing toward areas of concern.
4.There are excellent compelling nuclear reactions documented and independently confirmed(find them yourself) for LENR, your half truth nonsense is not compelling.
5.Coulomb barrier was a major objection to LENR observations and apparently still is. WL explanations and others are reasonable. Yet, nothing overcomes old school financially biased book thumpers with bad assumptions. Get a clue, follow the money.
6.That old school physics does not understand multi body interactions, shielded coulomb barriers, black holes, black energy, gravity, virtual particles, scientific method, long term non-equilibrium Hamiltonians, monetary bias, and LENR research is testimony enough.
7.Get out there and do some open minded real observational science, not this bias crap.
I have always believed that harmonics, within the lattice, may create standing waves that converge at points within the structure (focusing energy), causing atoms (or elements of atoms) to converge or change.
Keep in mind that I am a high school drop-out, 55 years old, with a sub-genius IQ. (which helps)
This guy has a bit of education though, and he has said this…
“Professor Takahashi thinks that what is occurring is not conventional fusion of two deuterium atoms but “a very unusual fusion” in which three or four hydrogen nuclei combine.
Such multi-body fusion is virtually unheard of but Dr. Takahashi has an elaborate theory to explain how the palladium could act as a scaffolding of sorts to hold the deuterium atoms in position so that three or more, when they start to vibrate, can fuse together. While he has some evidence to support his hypothesis, it is still just one of many unproven theories.”
From…
“Cold Fusion, Derided in U.S., Is Hot In Japan”
By ANDREW J. POLLACK
Published: November 17, 1992
http://www.nytimes.com/1992/11/17/science/cold-fusion-derided-in-us-is-hot-in-japan.html?pagewanted=all&src=pm
Conventional (fusion) physics may not grasp or explain all phenomenon.
A convention is a selection from among two or more alternatives, where the rule or alternative is agreed upon among participants. Often the word refers to unwritten customs shared throughout a community. For instance, it is conventional in many societies that strangers being introduced shake hands. Some conventions are explicitly legislated; for example, it is conventional in the United States and in Germany that motorists drive on the right side of the road, whereas in England, Australia, Mauritius, and Barbados they drive on the left. The standardization of time is a human convention based on the solar cycle or calendar. The extent to which justice is conventional (as opposed to natural or objective) is historically an important debate among philosophers.
The nature of conventions has raised long-lasting philosophical discussion. Quine, Davidson, and David Lewis published influential writings on the subject. Lewis’s account of convention received an extended critique in Margaret Gilbert’s On Social Facts (1989), where an alternative account is offered. Another view of convention comes from Ruth Millikan’s Language: A Biological Model (2005), once more against Lewis.
The Buddha described conventions — whether linguistic, social, political, moral, ethical, scientific, logical, or even religious — as arising dependent on specific conditions. According to his paradigm, when conventions are considered absolute realities, they contribute to dogmatism, which in turn leads to conflict. This does not mean that conventions should be absolutely ignored as unreal and therefore useless. Instead, according to Buddhist thought, a wise person adopts a middle way without holding conventions to be ultimate or ignoring them when they are fruitful.
joshua,
In reply
1.The science needs to be done not ignored or covered up by biased parties.
2.High field strength and many mechanisms are adequate, your answer is nonsense.
3.LENR is a new field about 5 years old based upon surface area rather than bulk lattice. Nanotechnology is expanding exponentially in knowledge especially in the last 5 years.
4.Milliwatts are more than the net yield of hot fusion. I demand calorimetry! The research bias is extreme for funding and lack of funding is representative of bias.
5.You admit to extreme funding bias.
6.Your dissembling answer shows you believe your equations more than observational science uncertainty based upon statistical residual error.
7.Throwing the pseudoscience label shows your extreme bias. Pretending you support bias free observational science is nonsense when you’ve already admitted extreme bias.
First, I suggest you look at the residual fuel from a LENR reactor to base your theory on: there are no shrunken atoms, just trans mutated ones. This strongly suggests neutron exchange, and where does the neutrons come from but from a proton and an electron joining together?
Second, the energy generated by the exothermic reaction is infrared (i.e. “heat”), not light generally.
Third, this LENR exothermic reaction is nuclear, and is taking place because of the close proximity of the hydrogen atoms (presumably).
Bottom line: all I care about is 6 orders of magnitude more energy density using very common fuel (hydrogen and nickel). Furthermore, all I care about is getting a LENR reactor on the market so we open the flood gates of talent to design more and better applications.
1. LENR is a proven exothermic physical phenomena.
2. LENR is nuclear in nature, and involves ultra-low momentum neutrons.
3. The neutrons are being created by the joining of a proton and an electron.
4. The missing mass-energy of the difference between the proton and the electron, and the neutron, is coming from somewhere.
5. Nuclear transmutation is taking place, as is evidenced by the residual LENR reactor fuel.
6. This process of nuclear transmutation is releasing energy via beta decay.
To Brad Arnold,
Dear Sir,
consider the article “Cold Fusion Catalyst” on the no longer existing website “e-Cat Site”
merged with “Cold Fusion Now” and ask Ben for a copy of the “sequel text” relating to the use of liquid lithium. An addendum mentioned in e-mail relates to the of use of negatively charged deuterium (D-) absorbed in electrically conductive metal particles (e.g. Pd and Ni) injected into positively charged liquid lithium (keV difference) for nuclear fusion driven by Coulomb explosion.
I read the article and the comments. I am far from qualified to response to the different calculations or theories discussed. I have followed the LENR discussion for a long time and believe it has some value, a value I should like to understand.
Instead I will comment on the discussion. I think there is a tremendous lack of humility. I do not think extensive schooling either as a scientist or lawyer makes you an expert. It does not even say that you are good at it. It merely says that you have passed through the education required to call yourself a lawyer or a scientist. Reason we accept that is because it is measureable. It fits the bureaucrats.
In my world there are other criteria that are more important.
As far as I know there is no clear evidence that LENR ever can be what we all want it to be. However, that can be said about many things we spend time energy and money to research.
A more important factor to me is the potential to positive improvements. In that regards LENR is in a class by itself and can only be compared to innovations like Gutenberg’s print press and similar. If we can spend research money (millions) on the relation between obesity among gay man and lesbians, I think a few billions to research LENR is well worth it. However, if we ever expect a result, we need to have people, which are positive to the potential to conduct the research, or the value of the research will be comparable to the obesity project.
I guess I will be told that I should not say anything as I am certainly not an expert. There is , however, a Swedish say: “Even a blind hen will eventually pick a corn”. Enthusiasm, persistent focus on positive result is at least as important. Another thing is that there is a incompetence competence. It is shown, that a mind with no preconceived knowledge, is more apt to see the unknown. Finally I have a definition of an expert: “ someone who knows everything about nothing”. I admit being a generalist: “who knows nothing about everything”.